Releasing the Time Step Upper Bound of CFL Stability Condition for the Acoustic Wave Simulation With Model-Order Reduction

Introduction

Numerical simulation of seismic wavefields is an important technical means to understand the law of seismic wave propagation and imaging underground complex structures. It is an essential theoretical basis for seismological research and plays an important role in seismology. Simulating the propagation of seismic waves by solving wave equations is the most widely used numerical simulation method. The explicit finite-difference (FD) scheme, the method of explicitly iterating the wavefield in the time domain, is widely used in seismic wavefield numerical simulation due to its simplicity (Etgen and O'Brien, 2007). The size of the time step can directly affect the calculation efficiency of the explicit FD scheme. For a given length of wavefield propagation time, a larger time step means fewer iterations than a smaller time step, which can improve the calculation efficiency. For the explicit FD scheme, two difficulties are observed when a large time step is adopted. First, the numerical simulation using a large time step leads to a numerical dispersion error, which can cause inaccurate amplitude and inaccurate phase information of the simulated seismic waveforms (i.e., time-dispersion error). Second, the time step size must be strictly limited by the Courant–Friedrichs–Lewy (CFL) stability condition (Courant et al., 1928), and a small time step must be accepted in practice to guarantee a stable numerical scheme for the numerical simulation of small-scale structures or high-velocity targets. Especially in the fine structure simulation, the small spatial grid makes the time step even smaller and increases computing complexity. Therefore, finding efficient large time-step numerical algorithms while ensuring the accuracy and stability has become a research hotspot in the field of seismic wavefield numerical simulation in recent years (Stork, 2013; Wang and Xu, 2015; Gao et al., 2016; Koene et al., 2018; Liu, 2020).

As mentioned before, to use a large time step for numerical simulation, the first problem to be handled is to eliminate the time-dispersion error caused by a large time step. In this aspect, researchers have conducted numerous studies in order to suppress the time-dispersion error; for a detailed review refer to Wang and Xu (2015) and Gao et al. (2016). A couple of previous methods for eliminating the time-dispersion error are achieved using higher precision temporal discretization schemes (Dablain, 1986; Kosloff et al., 1989; Chen, 2007; Song and Fomel, 2011). Stork (2013) demonstrated that the time-dispersion error only depends on the frequency, time step size, and total propagation time. The time-dispersion error is independent of both the velocity model and the space dispersion. Therefore, the time dispersion can be handled separately from the space dispersion without considering velocity variations. Based on these theories, Stork (2013) proposed a novel idea to eliminate the time-dispersion error: it is predictable and can be removed by a time-varying filter and interpolation after FD modeling (Dai et al., 2014; Liu et al., 2014; Li et al., 2016).

As a further development of Stork’s work, Wang and Xu (2015) constructed analytical time-varying filters with a conventional explicit FD scheme, entitled the time-dispersion transform method. This method includes a time-dispersion prediction algorithm (forward time-dispersion transform, FTDT) and a time-dispersion elimination algorithm (inverse time-dispersion transform, ITDT) to add and remove the time-dispersion error flexibly. Koene et al. (2018) modified the FTDT algorithm and constructed a complete process to remove time-dispersion error for seismic wave numerical simulation by applying FTDT to the source time function before the simulation and applying ITDT to the output waveforms after the simulation. FTDT is preprocessing and ITDT is post-processing, neither of which participates in the iteration of the wavefield and does not affect the main body of the wavefield numerical simulation. The time-dispersion transform method can effectively eliminate the time-dispersion error and can provide a guaranteed accuracy for numerical simulation using a large time step. The total calculation amount of the simulation is less than that of the conventional wavefield simulation with the same accuracy.

The time-dispersion transform method allows us to use a time step size close to the stability condition for numerical simulation without worrying about the inaccuracy caused by the time-dispersion error (Gao et al., 2016; Koene et al., 2018). Then the CFL stability condition becomes the main limitation if a large time step for the explicit FD scheme is used. In recent years, researchers turn to figure out appropriate numerical strategies for releasing the time step size beyond the CFL stability upper bound, which certainly draws attention in the seismic simulation community.

Ecer et al. (2000) proposed that when a time step was beyond the CFL stability upper bound, the unstable component would appear in the high-wavenumber region. Therefore, the instability of the high-wavenumber region can be measured by a spatial filtering algorithm and using a low-pass filter to filter out the unstable components generated in the high-wavenumber area. Later on, Sarris (2011) adopted the spatial filtering algorithm to solve the instability problem for solving Maxwell’s equation in the field of electromagnetic wave numerical simulation. Also, the time step of the explicit FD scheme can be successfully released beyond the CFL stability upper bound (Chang and Sarris, 2011; Chang and Sarris, 2012, 2013).

In the field of electromagnetic wave numerical simulation, He et al. (2012) proposed an unconditionally stable method by eigenvalue operation of the updated matrix based on the explicit FD scheme. Gaffar and Jiao (2014, 2015) analyzed the instability when using a time step that exceeds the CFL stability condition of the explicit FD scheme. The unstable eigenvalues are then abandoned from the initial numerical system before the explicit time iteration (Yan and Jiao, 2017), called the eigenvalue abandonment algorithm. Li et al. (2014) implemented the unconditionally stable method by perturbing the modulus of the unstable eigenvalues to be stable, instead of abandoning them, which is called the eigenvalue perturbation algorithm (Li, 2014). Since both methods of removing and perturbing the unstable eigenvalues are preprocessing algorithms, they have little effect on the calculation amount of the wavefield iteration process.

Inspired by the abovementioned explicit unconditionally stable numerical simulation methods, Gao et al. (2018, 2019) introduced the eigenvalue perturbation method and the spatial filtering method to seismic wave numerical simulation, respectively. Meanwhile, the time-dispersion error caused by a large time step was successfully eliminated by the time-dispersion transform method. The combination of eigenvalue perturbation and the time-dispersion transform method is suitable for strong heterogenous media. It can extend the available time step size toward the upper bound of the Nyquist sampling, saving many iterations while ensuring the calculation accuracy (Gao et al., 2018; Lyu et al., 2021).

Although the unconditionally stable algorithms for the explicit FD scheme have been applied in seismic wave numerical simulation, the related algorithms still need to be further modified and improved. The spatial filtering method bears the risk of unreluctantly filtering out the effective wavenumber when the wave propagates at a low velocity but in a strong heterogenous media. The abovementioned eigenvalue operation algorithms are all implemented based on discretizing the wave equation using a global matrix-form operator, which requires a huge amount of memory and computation during the temporal iteration progress of the wavefield for the numerical simulation. Meanwhile, to our knowledge, no literature that compares the effects of the eigenvalue abandonment algorithm and the eigenvalue perturbation algorithm is available to date, neither the selection criteria on how to choose these two methods.

In order to avoid the calculation of the global update-matrix operators during the wavefield iteration progress for the abovementioned eigenvalue operation algorithms, people adopted the model-order reduction (MOR) method (Remis and Van den Berg, 1998; Freund, 2004). The MOR method is implemented by the Krylov subspace projection of the space discretized dynamical system, which can project the original higher-state subspace into a significantly reduced-state subspace. This method captures the most influential eigenvalues of the dynamical system and can guarantee the dynamics of interest with sufficient accuracy. The MOR method has been widely used in the field of numerical simulation for electromagnetic waves and can be well coupled with eigenvalue operation algorithms to release the time step upper bound of CFL stability condition (He et al., 2012; Li, 2014; Gaffar and Jiao, 2014, 2015; Chen et al., 2016; Zhang et al., 2017). The MOR method has also been applied in the field of seismic wavefield numerical simulation in recent years (Pereyra and Kaelin, 2008; Pereyra, 2013; Wu et al., 2013; Basir et al., 2015; Pereyra, 2016; Basir et al., 2018), while no related literature in the field of seismic wavefield numerical simulation discussed extending the limit of CFL stability condition based on the MOR method.

This study introduces the MOR method to solve the scalar wave equation. First, we applied the eigenvalue decomposition to the update matrix for the discrete wave equation based on a given time step. Then we used only the update matrix’s eigenvalues and the expansion coefficients of the variables in the wave equation during the time step iteration. It can reduce the excessive dependence on the calculation memory for the wavefield iteration. To release the CFL stability upper bound, we brought forward the eigenvalue abandonment algorithm (He et al., 2012; Gaffar and Jiao, 2015) and the eigenvalue perturbation algorithm (Li, 2014; Gao et al., 2018; Lyu et al., 2021) to operate on the unstable eigenvalues of the update matrix, respectively. The workflows and characteristics of these two methods are introduced and compared in detail. The time-dispersion transform method is presented to eliminate the time-dispersion error caused by the large time step and ensure the accuracy of the numerical simulation (Wang and Xu, 2015; Koene et al., 2018). The FTDT is applied to the source time-discrete scheme during preprocessing, and the ITDT is applied to the seismic waveform during post-processing. Numerical experiments verify that the integration of the MOR method, the eigenvalue abandonment (and the eigenvalue perturbation), and the time-dispersion transform method can simulate highly accurate waveforms when a time step beyond the CFL stability upper bound is accepted. Our proposed numerical method is suitable for strong heterogenous media and can successfully surpass the time step size to the upper bound of the Nyquist sampling.

Methodology

Scalar Wave Equation and Its Discretization

Consider the following 2D scalar wave equation:

where $u$ and $c$ are the wavefield and the propagation velocity, respectively, and $s$ is the source term. With the second-order finite-difference (FD) method for the temporal discretization, the matrix form of Eq. 1 can be written as (Gao et al., 2018) follows:

where $U^{n+1}$ and $U^n$ represent the column vectors that collect the value of the wavefields at all grid nodes at the time $\left(n+1\right)\Delta t$ and $n\Delta t$, respectively; the column vector ${\overline{S}}^n=c^2\Delta t^2{S}^n$ and $S^n$ contains entries corresponding to the source location and source time function, respectively; and the size of the update matrix $\mathbf{M}$ is ${\left(N_x\times N_z\right)}^2$, where $N_x$ and $N_z$ are the grid numbers of discrete points along the x- and z-directions, respectively. After applying the Fourier transform in the time domain, the left-hand side of Eq. 2 in the frequency domain can be expressed as (Gao et al., 2018) follows:

where $\tilde{U}$ represents the forward Fourier transform of the wavefield $u$. Obviously, the range of the left-hand side of Eq. 2 is from $-4$ to 0. The matrix $\mathbf{M}$ is a semi-negative definite matrix, and its eigenvalues are non-positive real numbers (Gaffar and Jiao, 2014; Li, 2014; Gao et al., 2018; Lyu et al., 2021). Therefore, the CFL stability upper bound for Eq. 2 is obtained by requiring $\left|{\epsilon }_i\right|\le 4$, where ${\epsilon }_i$ is the eigenvalue of the update matrix $\mathbf{M}$, and the subscript i ranges from 1 to ${\left(N_x\times N_z\right)}^2$.

Model-Order Reduction

The MOR method can be realized by singular value decomposition (Pereyra and Kaelin, 2008; Li, 2014) or eigenvalue decomposition (Gaffar and Jiao, 2014, 2015; Basir et al., 2015, 2018). The former method can handle a non-square matrix, while the latter method can only handle a square matrix. The update matrix $\mathbf{M}$ is a square matrix, and it is completely applicable to eigenvalue decomposition, whose calculation is smaller and more concise than that of the singular value decomposition. Therefore, we adopted the eigenvalue decomposition method to implement the MOR method.

To introduce the MOR method, we first performed eigenvalue decomposition on the update matrix $\mathbf{M}$ as follows:

where the matrix $\mathbf{V}$ contains the eigenvectors $V_i$ of matrix $\mathbf{M}$, while $E$ is a diagonal matrix whose entries are the eigenvalues ${\epsilon }_i$ of matrix $\mathbf{M}$. We used the eigenvalues ${\epsilon }_i$ in matrix $\mathbf{E}$ to form a column vector $E$. Using the MOR method, Eq. 2 can be abbreviated as follows:

where $A^n$ and $B^n$ are the column vector of expansion coefficients for $U^n$ and ${\overline{S}}^n$, respectively; $U^n=\mathbf{V}{A}^n={\displaystyle \sum _i{\alpha }_i^n{V}_i}$ and ${\overline{S}}^n=\mathbf{V}{B}^n={\displaystyle \sum }_i{\beta }_i^n{V}_i$, where the expansion coefficients ${\alpha }_i^n$ and ${\beta }_i^n$ are the ith element of the column vector $A^n$ and $B^n$, respectively. $V_i$ is the ith column vector of the eigenvector matrix $\mathbf{V}$; the calculation symbol “$.\ast$” represents multiplying the corresponding elements for the column vectors on both sides.

Column vectors $A^n$, $A^{n-1}$, $E$, and $B^n$ in Eq. 5 are the input for the wavefield solving iteration, and $A^{n+1}$ is the output for the iteration. After each iteration, we can obtain the updated wavefield by the following equation:

The calculation of Eq. 6 can output the global wavefield values, including all the spatial grid points. If we only need to output the wavefield values of a certain trace at a fixed point, we do not need to calculate Eq. 6. For example, to output the wave value at a fixed point $\left(x_{out}, z_{out}\right)$ ($x_{out}$ and $z_{out}$ are the corner marks along the x- and z-direction in the discrete coordinate, respectively), we can use the $\left[(z_{out}-1)\times N_x+x_{out}\right]$ th row vector in matrix $\mathbf{V}$ and multiply by $A^{n+1}$, whose calculation amount is very small.

The input expansion coefficients $B^n$ for the source are obtained by $B^n={\mathbf{V}}^{-1}{\overline{S}}^n$. Generally, the source is located at a fixed location, that is, the column vector ${\overline{S}}^n$ contains only one element $s^n$ that corresponds to the source; other elements are all zero. The position of the element $s^n$ determines the location of the source, and the value of the element $s^n$ represents the value of the source time function at time $n\Delta t$. Source column vectors ${\overline{S}}^{n+1}$ and ${\overline{S}}^n$ at adjacent moments only have one different element with a scalar factor ratio $\alpha$ (e.g., ${\overline{S}}^{n+1}=\alpha {\overline{S}}^n$), which is determined by the amplitudes of the source time function at different times. Therefore, there is no need to perform the matrix calculation $B^n={\mathbf{V}}^{-1}{\overline{S}}^n$ for each iteration. We only need to know the ratio $\alpha$ of the source time function at adjacent moments, and the expansion coefficients $B^{n+1}$ can be obtained by $B^{n+1}=\alpha B^n$.

We can see that only the eigenvalues $E$ of the updated matrix and the expansion coefficients $A^n$, $A^{n-1}$, and $B^n$ (wavefield and source) in Eq. 5 are used to do the iteration of wave propagation, which is just an iteration of the column vectors and greatly simplifies numerical simulation compared with Eq. 2.

Releasing the Time Step Upper Bound of the CFL Stability Condition

We used the fourth-order FD method for the spatial discretization of $\mathbf{M}$ in Eq. 2. Using the velocity c = 4,000 m/s and the spatial grid interval Δx = Δz = h = 10 m, we can obtain the maximum time step $\Delta t_{\text{max}}$ = 1.530 ms, according to the CFL stability condition for high-order FD schemes (Liu and Sen, 2009). For a time step Δt over $\Delta t_{\text{max}}$, the discrete update matrix $\mathbf{M}$ will contain unstable eigenvalues (Li et al., 2014; Gao et al., 2018; Lyu et al., 2021). As shown in Figure 1, the eigenvalues of the discrete update matrix for $\Delta t=1 \text{ms}$ are all distributed in the range of 0 to −4, which means that all the eigenvalues are stable (Gao et al., 2018); in contrast, some eigenvalues of matrix $\mathbf{M}$ for the time step larger than $\Delta t_{\text{max}}$ (e.g., Δt = 2, 3, 4, 5, 6, 7, 8, and 9 ms) are distributed outside of the range of 0 to −4 (the red zones showed in Figure 1). These eigenvalues, whose absolute values violate the basic requirement of $\left|{\epsilon }_i\right|\le 4$, cause unstable phenomena when $\Delta t>\Delta t_{\text{max}}$. Table 1 shows the number of stable eigenvalues for different time steps. We can see that after the time step exceeds $\Delta t_{\text{max}}$, the number of stable eigenvalues decreases sharply as the time step increases (e.g., when Δt = 9 ms, only 965 stable eigenvalues exist, which is 2.39% of the total numbers 40401). To release the CFL stability upper bound on the time step, we introduced two kinds of operations for those unstable eigenvalues of matrix $\mathbf{M}$: the eigenvalue abandonment algorithm and the eigenvalue perturbation algorithm.

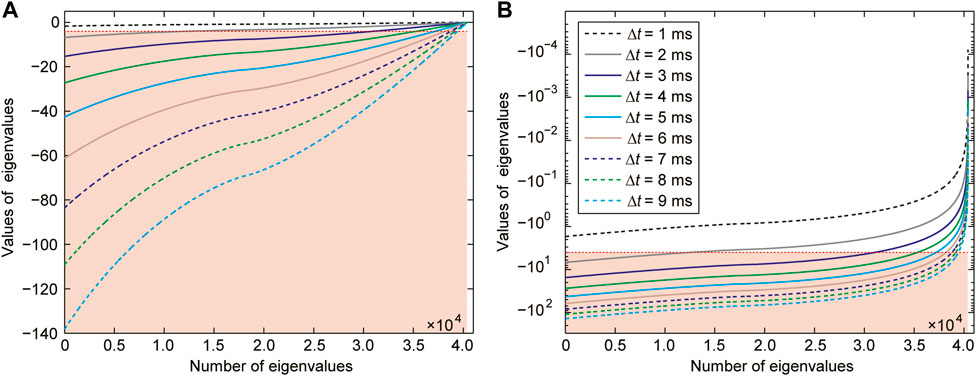
FIGURE 1. Eigenvalues of the discrete update matrix $\mathbf{M}$ for different time steps. (A) The eigenvalues for time steps of Δt = 1, 2, 3, 4, 5, 6, 7, 8, and 9 ms. (B) Logarithmic display for the eigenvalues in (A).

TABLE 1. Number of stable eigenvalues for the discrete update matrix $\mathbf{M}$ for different time steps. The table is generated using the second-order temporal FD scheme and the fourth-order spatial FD scheme, with the velocity $c=4000$ m/s and the spatial grid interval $h=10$ m.

Eigenvalue Abandonment

We used the eigenvalues ${\epsilon }_i$ in the diagonal matrix $E$ to form a column vector $E$, which can be divided into two parts (He et al., 2012; Gaffar and Jiao, 2015) as follows:

where $E_s$ is the column vector that consists of the stable eigenvalues, and $E_u$ is the column vector that consists of the unstable eigenvalues. We classified the eigenvectors in matrix $V$ according to Eq. 7, and matrix $V$ can be expressed as follows:

where matrix ${\mathbf{V}}_s$ and matrix ${\mathbf{V}}_u$ are composed of the eigenvectors ${\mathbf{V}}_i$ that correspond to the eigenvalues ${\epsilon }_i$ in $E_s$ and $E_u$, respectively.

The eigenvalue abandonment algorithm (He et al., 2012; Gaffar and Jiao, 2015; Chen et al., 2016) is implemented by abandoning the unstable eigenvalues $E_u$ and the corresponding eigenvectors ${\mathbf{V}}_u$; while only the column vector is composed of stable eigenvalues $E_s$, the corresponding eigenvector ${\mathbf{V}}_s$ participates in the iteration of wavefield calculation. After the eigenvalue abandonment operation, Eq. 5 can be expressed as follows:

where the number of elements in the column vectors $A_s^{n+1}$, $A_s^n$, $A_s^{n-1}$, and $B_s^n$ is equal to the number of elements in the column vector $E_s$. We can obtain the updated wavefield by $U^{n+1}={\mathbf{V}}_s{A}_s^{n+1}$ after each iteration. The input expansion coefficients $B_s^n$ for the source term are obtained by $B_s^n={\mathbf{V}}_s^{-1}{\overline{S}}_s^n$. The whole workflow for the wavefield iteration using Eq. 9 is shown in Figure 2A.

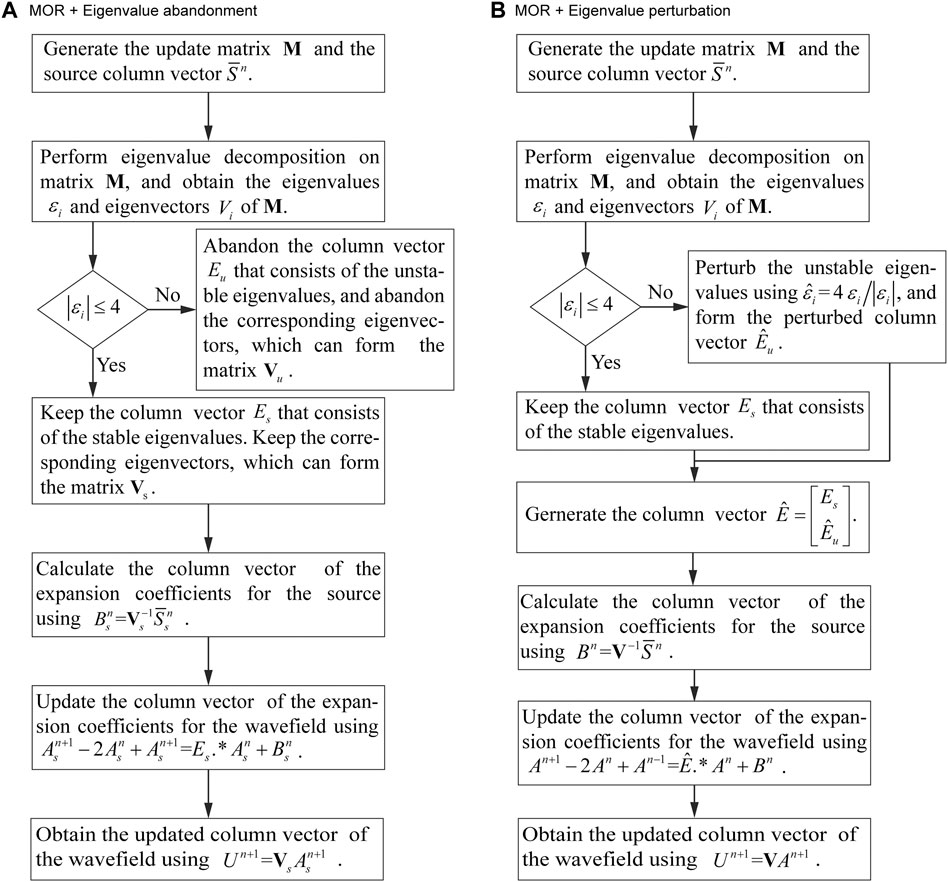
FIGURE 2. Workflows for releasing the CFL stability limit on the time step for numerical simulation based on the MOR method using eigenvalue operations. (A) Workflow for the numerical simulation using eigenvalue abandonment. (B) Workflow for the numerical simulation using eigenvalue perturbation.

Eigenvalue Perturbation

For the detailed description for the eigenvalue perturbation process refer to Li et al. (2014) and Gao et al. (2018). Here, we introduced the eigenvalue perturbation algorithm combined with the MOR method. The unstable eigenvalues of $\mathbf{M}$ (${\epsilon }_i$ in column vector $E_u$) that violate $\left|{\epsilon }_i\right|\le 4$ can be perturbed by the following :

In this way, the magnitude of the unstable eigenvalues is normalized to −4, which can guarantee the stability when using a time step beyond the CFL stability upper bound. The perturbed eigenvalues are collected to form a new column vector ${\widehat{E}}_u$, which can form the new matrix column vector $\widehat{E}$ with the originally stable eigenvalues column vector $E_s$, as follows:

After the eigenvalue perturbation operation, Eq. 5 can be expressed as follows:

The calculation process of Eq. 12 is as same as that of Eq. 5, except for using $\widehat{E}$ to replace $E$. The whole workflow for the wavefield iteration using Eq. 12 is shown in Figure 2B.

Eliminating the Time-Dispersion Error

We used the time-dispersion transform method, which includes the forward time-dispersion transform (FTDT) algorithm and the inverse time-dispersion (ITDT) algorithm (Wang and Xu, 2015; Koene et al., 2018). For a detailed description of the time-dispersion transform method process refer to Koene et al. (2018). The whole workflow of the time-dispersion error elimination using the time-dispersion transform method is shown in Figure 3.

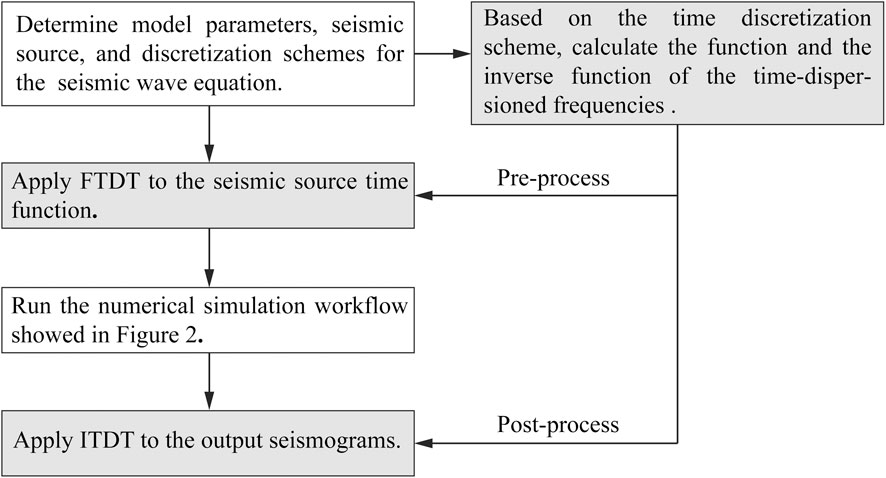
FIGURE 3. Workflow for the time-dispersion error elimination using the time-dispersion transform method.

Numerical Experiments

Homogenous Model

We performed numerical experiments on a homogenous square model by the finite-difference time-domain method. The wave velocity is c = 4,000 m/s. The spatial grid interval is Δx = Δz = 10 m, and the grid point number is 201 × 201. The source is a Ricker wavelet with a dominant frequency of 20 Hz, which is located at x = 1.0 km and z = 1.0 km. According to the CFL stability condition, the maximum time step for the second-order FD method in temporal discretization and fourth-order FD method in spatial discretization is $\Delta t_{\text{max}}$ = 1.530 ms. We tested several large time steps (Δt = 2, 3, 4, 5, 6, 7, 8, and 9 ms) by Eqs. 9–12, where all time steps are beyond the CFL stability upper bound. We used the workflow in Figure 3 to apply the time-dispersion transform method. To examine the results obtained by the different time steps, we performed numerical simulations using a short time step Δt = 1 ms, which is also applied by the time-dispersion transform method. The simulated waveforms can be regarded as theoretical references to examine the accuracy using larger time steps.

Figure 4 shows the waveforms recorded at x = 700 m and z = 700 m. Although the time steps exceed the CFL stability condition, no instability arises after applying the eigenvalue abandonment (shown in Figure 4A) and the eigenvalue perturbation (shown in Figure 4B). It proves that the combination of the MOR, eigenvalue abandonment (and eigenvalue perturbation) algorithm, and time-dispersion transform methods can extend the CFL stability upper bound successfully.

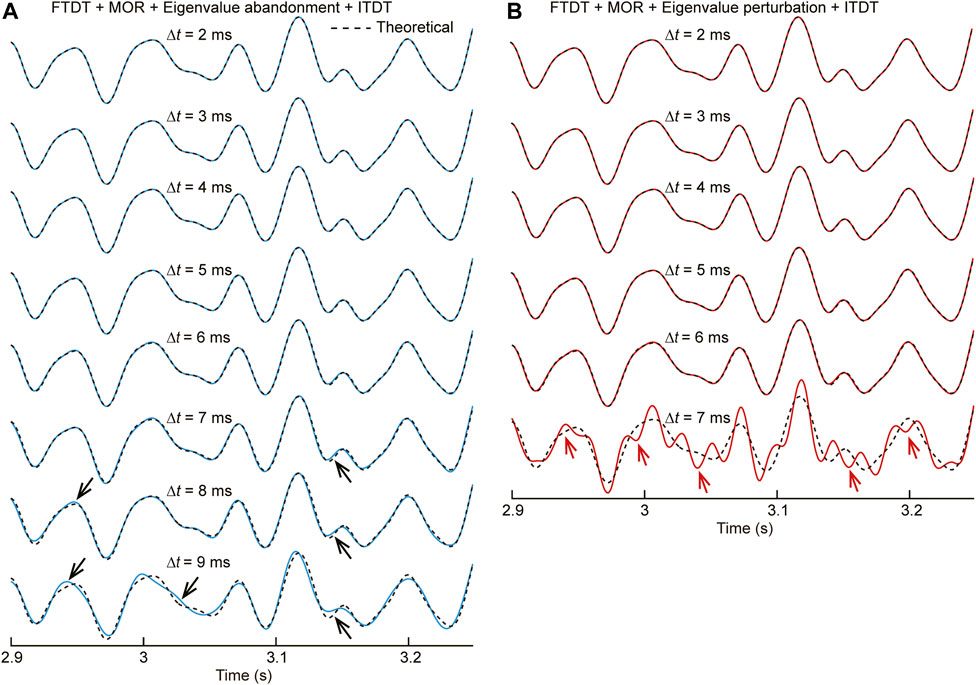
FIGURE 4. Waveforms that are recorded at a fixed point (x = 700 m, z = 700 m) of the homogenous model using different time steps. The dashed curve obtained using Δt = 1 ms (with the time-dispersion transform method applied) is taken as the theoretical reference. Eight and six time steps are tested for eigenvalue abandonment and eigenvalue perturbation, respectively. The waveforms in (A) are obtained using the eigenvalue abandonment algorithm, and the waveforms in (B) are obtained using the eigenvalue perturbation algorithm. All the waveforms are the final results after the time-dispersion transform method has been applied according to the workflows showed in Figure 3.

The time-dispersion error using Δt = 2, 3, 4, 5, and 6 ms is invisible, as shown in Figures 4A,B. It indicates that integration of the MOR, eigenvalue abandonment (or eigenvalue perturbation) algorithm, and the time-dispersion transform method can provide highly accurate simulation results even when a much larger time step size beyond the CFL stability upper bound is used.

According to the Nyquist sampling theorem $\Delta t<1/\left(2f_{\text{max}}\right)$ (Gaffar and Jiao, 2014; Gao et al., 2018), the time step size cannot be larger than 6.7 ms for the Ricker wavelet with a dominant frequency of 20 Hz, whose maximum frequency is about 75 Hz. Therefore, using Δt = 7 ms has exceeded the Nyquist sampling. Interestingly, starting from Δt = 7 ms, the results of the two processing methods are different. Although 7 ms has exceeded the Nyquist sample for the eigenvalue abandonment operation, the results still seem acceptable except for some slight error. We need to associate the eigenvalue abandonment with the spatial filtering method (Gao et al., 2019). Different eigenvalues of the updated matrix correspond to different wavenumbers: the unstable eigenvalues correspond to the wavefield that distributes in the high-wavenumber region, and stable eigenvalues correspond to the low-wavenumber region (Li, 2014). Abandoning the unstable eigenvalues is equivalent to filtering out the unstable wavefield components with a low-pass filter. The aliasing effect caused by insufficient sampling points (i.e., using a time step that exceeds the Nyquist sampling upper bound) is a high-frequency oscillation, which would be filtered out by a low-pass filtering operation.

In contrast, the eigenvalue perturbation operation is implemented by perturbing the unstable eigenvalues into stable eigenvalues, which is a normalized operation, rather than a low-pass filter. The high-frequency oscillation caused by insufficient sampling points will be retained. It can explain why the high-frequency oscillation exists resulting from the eigenvalue perturbation algorithm using Δt = 7 ms in Figure 4B.

Next, using the idea of spatial filtering, it is easy to explain the inaccuracy for the result obtained using Δt = 9 ms in Figure 3A. As the time step increases, the number of stable eigenvalues decreases dramatically (as shown in Table 1). It is equivalent to a sharp decrease in the threshold of the low-pass filter for spatial filtering. The effective seismic wavefield mainly distributes in a certain bandwidth of low wavenumber. The corresponding low-pass filter would filter out the effective wavefield distributes in the low-wavenumber regions for an excessively large time step. As a result, the wavefield information is incomplete. Even if the time-dispersion transform method is used, the result would still have errors.

We further analyzed the amplitude errors between the waveforms obtained by different time steps and the theoretical waveform (as shown in Figure 5). The time ranges from 3 to 3.1 s, which is an intermediate time period of the waveforms in Figures 4, 5C,D, are logarithmic displays for the absolute values of the amplitude errors in Figures 5A,B, respectively. The amplitude errors increase with the increasing time step, but the errors are acceptable when Δt ≤ 6 ms. For example, using Δt = 2 ms, the values of amplitude errors are around 0.001 (red lines in Figures 5C,D), while the amplitude values of the theoretical waveform range from −3.340 to 4.011, and the error of 0.001 is negligible relative to the overall amplitude values; using Δt = 6 ms, the maximum error is about 0.1 (grey lines in Figures 5C,D), which is only 2.5% of the maximum amplitude value 4.011.

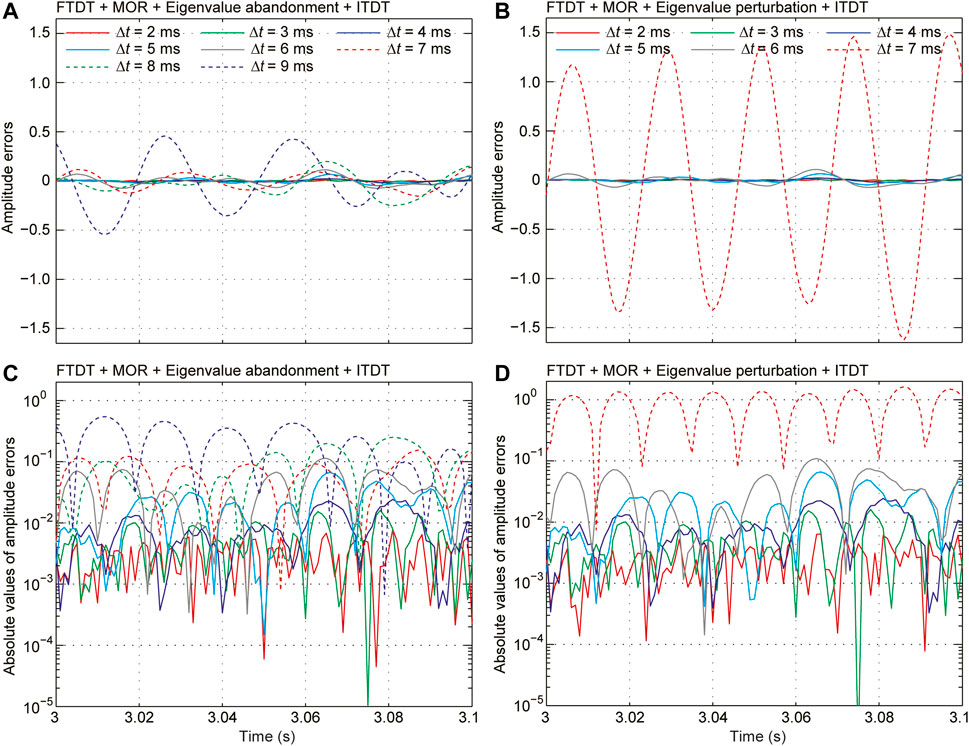
FIGURE 5. Amplitude errors between the waveforms and the theoretical waveform showed in Figure 4 (from 3 s to 3.1 s). The amplitude errors in (A) and (B) are obtained using the eigenvalue abandonment algorithm and the eigenvalue perturbation algorithm, respectively. (C) and (D) are logarithmic display for the absolute values of the amplitude errors in (A) and (B), respectively.

Based on the analysis mentioned before, for a homogenous model, in association with the MOR method and the time-dispersion transform method, both the eigenvalue perturbation algorithm and the eigenvalue abandonment algorithm can release the time step toward the upper bound of the Nyquist sampling and still ensure the accuracy of the numerical simulation. For the eigenvalue abandonment operation, although no high-frequency oscillations appear after the time step size exceeds the Nyquist sampling, there is a risk of filtering out effective wavefield that distributes in the low-wavenumber region if the time step size is too large.

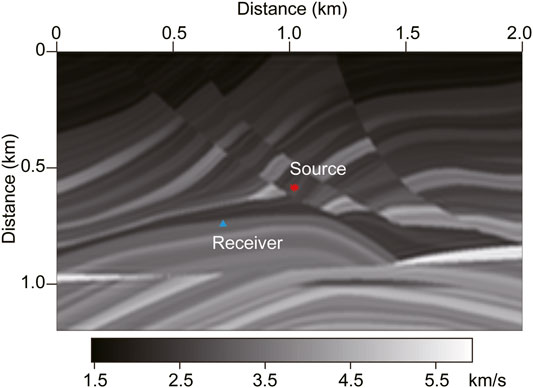
Heterogenous Model

We verified the feasibility of the proposed methods by a heterogenous medium, part of the Marmousi model, as shown in Figure 6. In this model, the velocity contrast is strong, the multiple waves are significant, and the velocity range is from 1,467 to 5,928 m/s. The spatial grid interval is Δx = Δz = 10 m, and the grid point number is 121 × 201. The source is a Ricker wavelet with a dominant frequency of 15 Hz, located at x = 1.0 km and z = 0.6 km. The maximum time step size for the second-order FD method in temporal discretization and the fourth-order FD method in spatial discretization schemes are $\Delta t_{\text{max}}$ = 1.032 ms. We tested several large time steps (Δt = 2, 3, 4, 5, 6, 7, 8, and 9 ms), and all these time steps are beyond the CFL stability upper bound. We used the workflow in Figure 3 to apply the time-dispersion transform method. Similar to what has been done in the heterogenous model, we performed numerical simulations using a small time step Δt = 1 ms, whose results can be regarded as theoretical references to examine the accuracy using larger time steps.

FIGURE 6. Modified Marmousi model.

Figure 7 shows the waveforms around 3 s. The residual errors are invisible even for the eigenvalue perturbation algorithm, even for Δt = 7 ms (shown in Figure 7B). Starting from Δt = 8 ms, the simulation results become inaccurate due to the time step size has exceeded the upper bound of the Nyquist sampling. It demonstrates that the combination of the MOR, the eigenvalue perturbation, and the time-dispersion transform method can still release the time step to the upper bound of the Nyquist sampling even for the heterogenous media with strong velocity contrast.

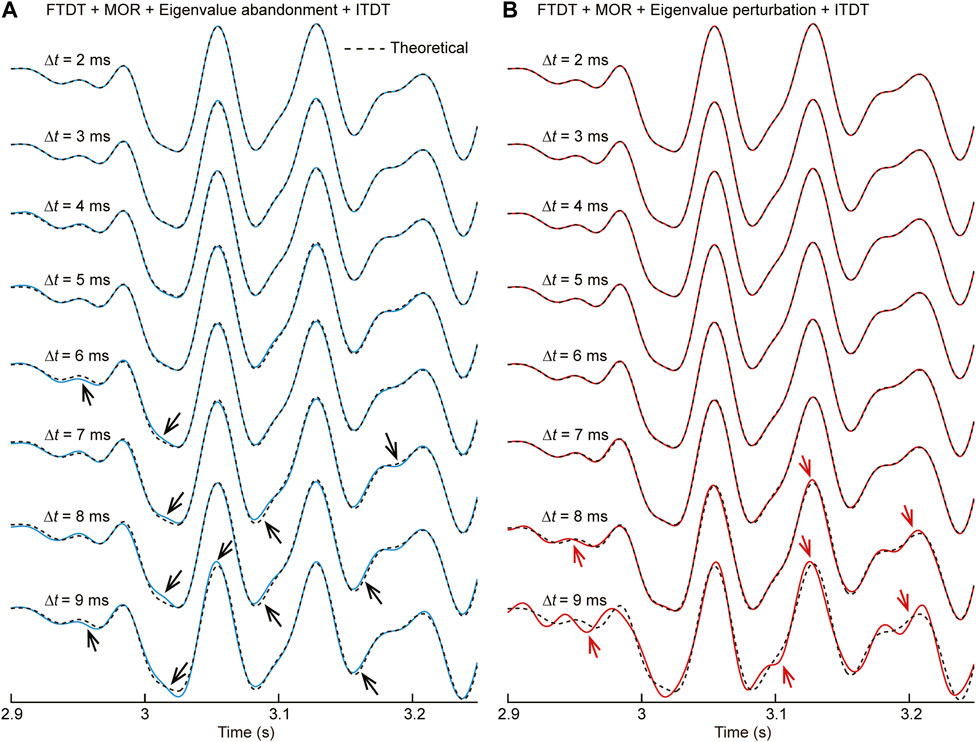
FIGURE 7. Waveforms that recorded at a fixed point (x = 700 m, z = 700 m) of the modified Marmousi model using different time steps. The dashed curve obtained using Δt = 1 ms (with the time-dispersion transform method applied) is taken as the theoretical reference. (A) Waveforms obtained using the eigenvalue abandonment algorithm. (B) Waveforms obtained using the eigenvalue perturbation algorithm. Eight time steps are tested: Δt = 2, 3, 4, 5, 6, 7, 8, and 9 ms, respectively.

For the eigenvalue abandonment algorithm, when Δt = 6 ms, a relatively obvious error appears. Simultaneously, the time step size has not reached the upper bound of the Nyquist sampling yet (shown in Figure 7A). This problem still needs to be explained from the perspective of the spatial filtering method. In heterogenous media, instability phenomenon would appear in the high-velocity region according to the CFL stability condition with the time step size increasing. Therefore, the threshold of the low-pass filter is determined by the high-velocity region. However, for the wavefield with a given bandwidth, the wavenumber range in the low-velocity region is wider than that in the high-velocity region (Gao et al., 2019). With the increasing time step size, the low-pass filter of the spatial filtering with decreasing threshold will filter out the effective wavefield in the low-velocity region, which would result in incomplete wavefield components. For the eigenvalue abandonment algorithm, when the time step size is too large (e.g., Δt ≥ 6 ms in this numerical experiment), the unstable eigenvalues are caused by the velocity in the high-velocity region, and this part of eigenvalues corresponds to the wavefield in the high-wavenumber region. Abandoning these unstable eigenvalues is equivalent to filtering out the wavefield of the corresponding wavenumber range, which would filter out the effective wavefield of the low-velocity region.

We further analyzed the amplitude errors between the waveforms obtained by different time steps and the theoretical waveform (as shown in Figure 8). The time ranges from 3 to 3.1 s, which is an intermediate time period of the waveforms in Figure 7. The amplitude values of the theoretical waveform range from −3.345 to 3.081. Using Δt = 6 ms, the maximum error of the eigenvalue abandonment algorithm is 0.204 (grey lines in Figures 8A,C), which is 6.1% of the maximum absolute amplitude value 3.345; while the maximum error of the eigenvalue abandonment algorithm is 0.059 (grey lines in Figures 8B,D), which is only 1.8% of the maximum amplitude value 3.345. Therefore, it is better to perturb this part of the eigenvalues to be stable than to abandon them directly, and this can retain the effective component of the wavefield. The eigenvalue perturbation algorithm is a better choice than the eigenvalue abandonment algorithm. The former is more suitable for the simulation of strongly heterogenous models. The time step can be released beyond the CFL stability upper bound and even toward the upper bound of the Nyquist sampling.

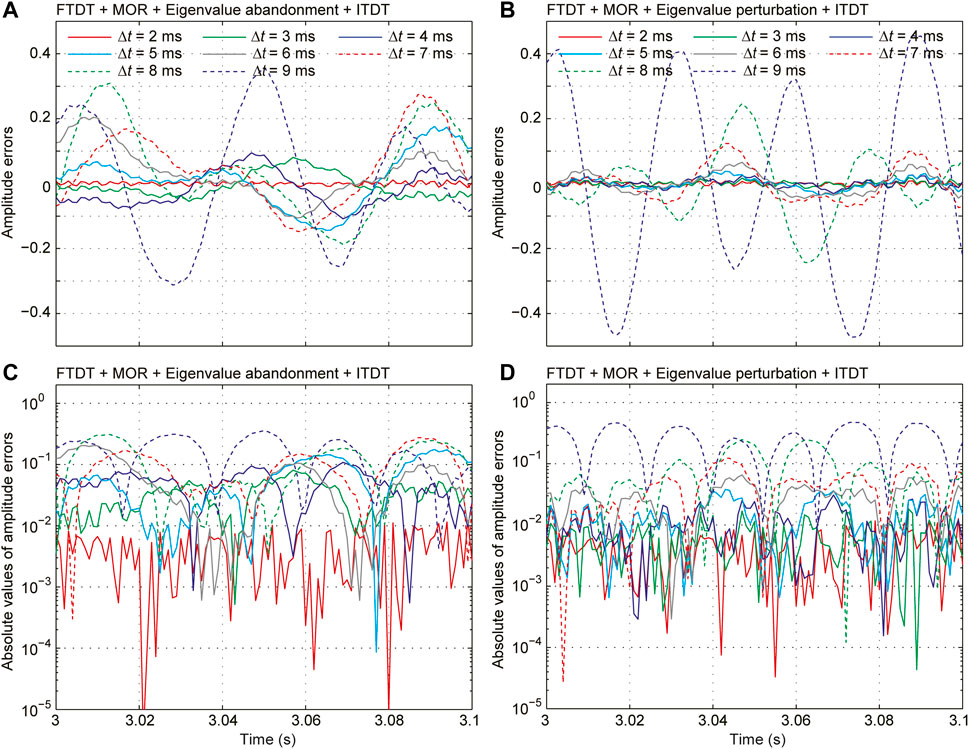
FIGURE 8. Amplitude errors between the waveforms and the theoretical waveform showed in Figure 7 (from 3 s to 3.1 s). The amplitude errors in (A) and (B) are obtained using the eigenvalue abandonment algorithm and the eigenvalue perturbation algorithm, respectively. (C) and (D) are logarithmic display for the absolute values of the amplitude errors in (A) and (B), respectively.

Discussions

In the Methodology section, we analyzed and manipulated the eigenvalues of matrix $M$ based on Eq. 2, whose stable eigenvalues range from 0 to −4. Equation 2 can also be written with the following alternative form Gao et al., 2018:

where $V^{n+1}$ and $V^n$ are the introduced auxiliary variables that represent the wavefields at $n\Delta t$ and $\left(n-1\right)\Delta t$, respectively (i.e., $V^{n+1}=U^n$ and $V^n=U^{n-1}$). According to the CFL stability condition, the stable eigenvalues of matrix $\mathbf{A}$ range from 0 to 1 (Gao et al., 2018). Since Eq. 13 is equivalent to Eq. 2, the range 0 to −4 for the stable eigenvalues of matrix $M$ is equivalent to the range 0–1 for the stable eigenvalues of matrix $A$. All the methods involved in this study can also be realized using Eq. 13. However, the size of matrix $M$ is ${\left(N_x\times N_z\right)}^2$, which is only a quarter of the size of the matrix $A$. This means Eq. 2 is more memory saving than Eq. 13. Therefore, we directly used Eq. 2 to introduce the relevant algorithms instead of starting with Eq. 13.

The limitation for the time step of the combination method using the eigenvalue abandonment algorithm is influenced by two factors: wavenumber range of the effective wavefield and the upper bound of the Nyquist sampling, which one is reached first depend on the model parameters. Furthermore, the combination method using the eigenvalue abandonment algorithm has the risk of filtering out the effective wavefield in the low-velocity region in the strongly heteronomous media, which is similar with the combination method using the spatial filtering method mentioned in Gao et al. (2019). The limitation for the time step of the combination method using the eigenvalue perturbation algorithm is only influenced by the upper bound of the Nyquist sampling, and this method is more suitable for strong heterogenous media (Gao et al., 2018). We preferred to use the combination method using the eigenvalue perturbation algorithm to release the time step upper bound of CFL stability condition.

The MOR method can effectively reduce the amount of calculation in the iterative process, but this skill is still implemented based on the global operator $M$. The eigenvalue decomposition calculation amount in preprocessing is still very large, especially for memory consumption, which is still a challenge faced by this method. Therefore, we still need to research how to release the time step size beyond the CFL stability condition by avoiding the global matrix operators in the future.

Conclusion

We introduced the model-order reduction (MOR) method to solve the acoustic wave equation. Only the updated matrix’s eigenvalues and the expansion coefficients of the variables in the wave equation are used to iterate the wave propagation, which greatly reduces the amount of calculation in the wavefield iteration process. Moreover, we introduced the eigenvalue abandonment algorithm and the eigenvalue perturbation algorithm to operate on the unstable eigenvalues of the updated matrix. We successfully released the time step size of the CFL stability condition for the explicit FD scheme. We then introduced the time-dispersion transform method to eliminate the time-dispersion error caused by the large time step and ensure numerical simulation’s accuracy. Numerical experiments show that the combination of the MOR method, eigenvalue abandonment (and the eigenvalue perturbation), and the time-dispersion method can simulate highly accurate waveforms when applying a time step beyond the CFL stability upper bound. The combination method using the eigenvalue abandonment algorithm has the risk of filtering out the effective wavefield in the low-velocity region in the strongly heteronomous media. The combination method using the eigenvalue perturbation algorithm is suitable for strong heterogenous media and can successfully extend the time step size toward the upper bound of the Nyquist sampling. An unusually sparse time step can be used for the seismic numerical simulation without suffering from the time-dispersion error and stability problems.

Author Contributions

YG derived the equations, wrote the program, and performed numerical experiments. M-HZ checked the formula derivation and performed analysis for the numerical experiments. HZ designed the experiments and analyzed the results of the numerical experiments.

Funding

This research was supported by the National Natural Science Foundation of China (grant nos. 41725017, 11773087) and the Science and Technology Development Fund, Macau SAR (grant nos. 0002/2019/APD, 0079/2018/A2). YG was also supported by the National Natural Science Foundation of China (grant no. 41704063) and the General Financial Grant from the China Postdoctoral Science Foundation (grant no. 2017M610980).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References